Introdução 🚀

Se você já se perguntou "mas que raio são limites no cálculo?", fique tranquilo: você não está sozinho! Limites são um dos conceitos mais importantes do cálculo, e dominar esse assunto é essencial para entender coisas como derivadas e integrais.

Seja você um estudante prestes a encarar um curso de cálculo ou apenas um curioso por matemática, este guia foi feito para tornar seu aprendizado mais tranquilo. Vamos nessa? 😃

Por Que Limites São Importantes? 🤔

Limites são a chave para desbloquear o mundo do cálculo! Eles nos ajudam a entender o comportamento das funções quando nos aproximamos de um determinado ponto. Sem eles, conceitos como derivadas e integrais simplesmente não existiriam! 😱

Se você pretende seguir carreiras em engenharia, física, ciência da computação ou qualquer outra área que envolva matemática avançada, aprender limites não é uma opção. É uma necessidade! 🚀

O Que Você Deve Saber Antes de Mergulhar nos Limites? 🏊

Antes de encarar os limites de frente, vale a pena conferir se sua base matemática está afiada. Aqui está um check-list rápido para garantir que você está pronto:

1. Entendimento de Funções 📈

Funções são os blocos de LEGO do cálculo. Sem elas, não conseguimos analisar limites de forma eficaz.

• Saiba como ler e escrever funções (por exemplo, $f(x)=x^{2}+3x−2$).
• Aprenda a avaliar funções (basta substituir valores na equação).
• Pratique a visualização de gráficos, pois isso vai te ajudar MUITO!

2. Álgebra: Sua Melhor Amiga 🤝

Se você tem dificuldades com álgebra, talvez seja um bom momento para revisar:

• Fatoração (vai aparecer o tempo todo!).
• Simplificação de expressões (evita cálculos desnecessários).
• Resolver equações (básico, mas essencial).

3. Trigonometria Básica 🔺

Funções trigonométricas como $\sin(x)$ e $\cos(x)$ aparecem o tempo todo nos limites. Então, é bom se familiarizar com:

• Círculo unitário (saber de cor os valores principais ajuda muito!).
• Identidades trigonométricas (como $\sin^2(x) + \cos^2(x) = 1$).
• Limites especiais, como:

4. Paciência e Prática 🧘

Ninguém aprende cálculo do dia para a noite. A prática constante é essencial! Não se frustre se não entender algo de primeira. Continue treinando, e logo você vai perceber que os limites começam a fazer sentido!

Vamos Começar! 🚀

Antes de mergulharmos, é importante notar que este artigo serve como um guia introdutório sobre limites, baseado na minha interpretação como um (quase) Engenheiro de Computação. Para aqueles que buscam um entendimento mais profundo e rigoroso, eu recomendo fortemente o livro Cálculo de James Stewart. Este livro é uma das referências mais completas e bem-estruturadas sobre o assunto, e muito do conhecimento compartilhado aqui é inspirado no trabalho de Stewart.

Agora que você já tem uma base, vamos explorar os limites com alguns exemplos práticos. A ideia é simples: descobrir qual valor $f(x)$ se aproxima quando $x$ se aproxima de um ponto específico.

Exemplo 1: Uma Função Linear Simples 🎯

Considere a função:

Qual é o limite de $f(x)$ quando $x$ se aproxima de 2?

Se você disse 4, parabéns! 🎉 Como essa é uma função contínua, basta substituir $x$ pelo valor desejado.

Exemplo 2: Função com um "Buraco" 🕳️

Agora, considere esta função:

Se tentarmos calcular $f(2)$ diretamente, encontramos uma indeterminação ($0/0$). O que fazer? 😲

A solução é fatorar o numerador:

Cancelamos os termos iguais e obtemos:

Agora, calculamos $\lim\limits_{x \to 2} f(x)$ simplesmente substituindo $x = 2$:

Embora a função original seja indefinida em $x = 2$, o limite ainda existe! 🔥

Curiosamente, essa função se comporta exatamente como $f(x) = x + 2$, exceto em $x = 2$, onde a função original é indefinida, pois o denominador se anula.

No entanto, ao calcular o limite, não nos preocupamos com o valor exato da função em $x = 2$, mas sim com seu comportamento nos arredores desse ponto. Em outras palavras, estamos interessados no que acontece quando x assume valores como $2.0000...1$ e $1.9999...$, e não no próprio $x = 2$.

Como a função $f(x) = x + 2$ descreve o comportamento da função original para todos os valores próximos de $x = 2$, podemos utilizá-la para analisar o limite de:

Boa notícia: é exatamente assim que nós, futuros engenheiros, encaramos os limites - substituindo funções complexas por outras que descrevem seu comportamento nas regiões de interesse! 🚀

Observação Importante: embora essas funções compartilhem o mesmo comportamento para todos os valores $x \neq 2$, elas não são idênticas. A função $f(x) = x + 2$ está definida para todo $x \in \mathbb{R}$, enquanto $f(x) = \frac{(x + 2)(x - 2)}{x - 2}$ possui um domínio restrito a $x \in \mathbb{R} \setminus \{2\}$.

Se plotarmos $f(x) = \frac{(x + 2)(x - 2)}{x - 2}$, veremos uma linha reta $y=x+2$ com um "buraco" em $x=2$. A função se aproxima cada vez mais de 4 quando $x$ se aproxima de 2, mas nunca realmente assume um valor em $x = 2$ porque a função é indefinida ali.

Mas Qual é a Definição Real de Limites? 🤔

Seja $f$ uma função definida em algum intervalo aberto que contém o número $a$, exceto possivelmente no próprio $a$. Então dizemos que o limite de $f(x)$ quando $x$ se aproxima de $a$ é $L$, e escrevemos

$$\lim_{x \to a} f(x) = L$$

se para todo número $\varepsilon > 0$, existe um número $\delta > 0$ tal que

$$\text{se \ } 0 \lt |x - a| \lt \delta \quad \text{então} \quad |f(x) - L| \lt \varepsilon.$$

(Stewart, et. al)

Eu sei, essa definição pode parecer um pouco intimidadora no início, com todas essas letras gregas e notações sofisticadas. Mas não se preocupe! Posso garantir que você não vai usá-la o tempo todo. Ainda assim, para o bem do conhecimento, vamos passar por um problema e ver como aplicá-la.

Exemplo ✨

Prove que $\lim\limits_{x \to 3} (4x - 5) = 7$

Solução 🚀

Vamos começar com a definição formal do limite:

Agora, reescrevendo a segunda parte:

O que nos dá:

Ou seja, isolando $|x - 3|$:

🔍 Escolha inteligente: Definimos $\delta = \frac{\varepsilon}{4}$ para garantir que a desigualdade seja satisfeita:

Assim, confirmamos que:

🎯 Conclusão: Pela definição formal, temos:

💡 Mas veja que na prática... Muitas vezes basta aplicar diretamente a substituição:

📌 Moral da história: A abordagem formal é fundamental para rigor matemático, mas a substituição direta nos lembra que os limites seguem a intuição! 😃

Certo! E Agora? 🤔

Vamos ver se você está acompanhando! Me diga, qual é este limite?

Se você tentou aplicar o método anterior, talvez tenha pensado:

🚨 Atenção! Isso não é matematicamente rigoroso! Mas calma, como futuros engenheiros, muitas vezes usamos notações informais para simplificar cálculos (como $\pi \approx 3.14$ e $g \approx 10$).

Para entender melhor, vamos observar alguns valores de $\frac{1}{|x|}$ conforme $x$ cresce:

🔍 Perceba que, à medida que $x$ aumenta, o resultado se aproxima cada vez mais de 0. Assim, faz sentido afirmar que:

Agora, vamos ver o que acontece quando $x$ se aproxima de 0:

📈 À medida que $x$ se aproxima de 0, $\frac{1}{|x|}$ cresce sem limites. Ou seja:

Agora, olhe para o gráfico abaixo! ⬇️

Existe alguma função sem limite em algum ponto? 🤔

Com certeza! Um exemplo clássico é a função $\frac{1}{x}$ quando $x \to 0$. Vamos analisar isso!

🔍 Perceba que o denominador agora é apenas $x$,ao invés de $|x|$.

🔎 Como podemos ver:

• Quando $x$ se aproxima de 0 pela esquerda ($\lim\limits_{x \to 0^{-}} \frac{1}{x}$), o valor da função vai para $-\infty$.
• Quando $x$ se aproxima de 0 pela direita ($\lim\limits_{x \to 0^{+}} \frac{1}{x}$), o valor da função vai para $+\infty$.

O que isso significa? 🤔

💡 Isso significa que esse limite não existe! Para que um limite exista em um ponto, os limites laterais devem ser iguais. Como isso não acontece aqui, dizemos que o limite em $x = 0$ não está definido.

Regra Geral para Limites em um Ponto 📏

$$\lim\limits_{x \to a} f(x) = L \quad \text{se e somente se} \quad \lim\limits_{x \to a^{-}} f(x) = L \quad \text{e} \quad \lim\limits_{x \to a^{+}} f(x) = L$$

(Stewart, et. al)

Ou seja, em palavras simples: o limite só existe se os limites laterais forem iguais! 🎯

O Teorema do Confronto: Uma Maneira Inteligente de Encontrar Limites Complicados 🤔

Às vezes, encontramos limites que são difíceis de resolver com as ferramentas que aprendemos até agora. Por exemplo, considere:

À primeira vista, esse limite parece complicado porque $\sin(x)$ oscila entre $-1$ e $1$ para sempre, enquanto $x$ cresce infinitamente. Como podemos determinar o que acontece com $\frac{\sin(x)}{x}$ quando $x$ se aproxima do infinito?

Intuição Primeiro

Vamos pensar sobre o comportamento de $\sin(x)$ e $x$:

• A função $\sin(x)$ está sempre limitada entre $-1$ e $1$, não importa o quão grande $x$ se torne.
• À medida que $x$ cresce para o infinito, o denominador $x$ se torna muito grande.

Isso significa que $\frac{\sin(x)}{x}$ é essencialmente um número muito pequeno (porque o numerador é no máximo $1$ e o denominador é enorme). Intuitivamente, podemos supor que:

Mas como podemos provar isso formalmente? Aqui entra o Teorema do Confronto!

O Teorema do Confronto

O Teorema do Confronto é uma ferramenta poderosa para avaliar limites que são difíceis de calcular diretamente. Aqui está o que ele diz:

Se $f(x) \leq g(x) \leq h(x)$ quando $x$ está próximo de $a$ (exceto possivelmente em $a$) e

$$\lim\limits_{x \to a} f(x) = \lim\limits_{x \to a} h(x) = L$$

então

$$\lim\limits_{x \to a} g(x) = L$$

(Stewart, et. al)

Em termos mais simples, se $g(x)$ está "espremida" entre duas funções $f(x)$ e $h(x)$ que ambas se aproximam do mesmo limite $L$, então $g(x)$ também deve se aproximar de $L$.

Aplicando o Teorema do Confronto a $\frac{\sin(x)}{x}$

Vamos usar o Teorema do Confronto para provar que:

1. Passo 1: Limitar $\sin(x)$
   Sabemos que $\sin(x)$ está sempre entre $-1$ e $1$:

   $$-1 \leq \sin(x) \leq 1$$

2. Passo 2: Dividir por $x$
   Como $x > 0$ (já que $x \to \infty$), podemos dividir a desigualdade por $x$ sem alterar o sentido das desigualdades:

   $$-\frac{1}{x} \leq \frac{\sin(x)}{x} \leq \frac{1}{x}$$

3. Passo 3: Aplicar Limites aos Limites
   Agora, considere os limites dos limites inferior e superior quando $x \to \infty$:

   $$\lim\limits_{x \to \infty}\left(-\frac{1}{x}\right) = 0 \quad \text{e} \quad \lim\limits_{x \to \infty}\frac{1}{x} = 0$$

4. Passo 4: Usar o Teorema do Confronto
   Como $\frac{\sin(x)}{x}$ está "espremida" entre $-\frac{1}{x}$ e $\frac{1}{x}$, e ambas essas funções se aproximam de $0$ quando $x \to \infty$, o Teorema do Confronto nos diz que:

   $$\lim\limits_{x \to \infty}\frac{\sin(x)}{x} = 0$$

Agora, veja esse comportamento no gráfico abaixo! ⬇️

Conclusão

O Teorema do Confronto é uma maneira inteligente de avaliar limites que são difíceis de calcular diretamente. Ao limitar uma função entre duas outras com limites conhecidos, podemos "espremer" o limite da função original. No caso de $\frac{\sin(x)}{x}$, usamos o fato de que $\sin(x)$ é limitada e $x$ cresce infinitamente para concluir que o limite é $0$.

Propriedades e Limites Especiais: Ferramentas para Facilitar sua Vida 🛠️

À medida que você se aprofunda no estudo de limites, encontrará certas propriedades e limites especiais que tornam a resolução de problemas muito mais simples. Embora as demonstrações formais dessas propriedades sejam mais avançadas, por enquanto, basta aceitá-las como verdades. Afinal, este é um guia introdutório, e você explorará as provas com mais detalhes em suas aulas de cálculo (e em livros como Cálculo, de James Stewart). Vamos dar uma olhada nessas ferramentas úteis!

Propriedades dos Limites

Os limites seguem certas regras que nos permitem decompor problemas complexos em partes mais simples. Aqui estão algumas propriedades fundamentais:

1. Regra da Soma/Diferença:
   O limite da soma (ou diferença) de duas funções é a soma (ou diferença) dos seus limites:

   $$\lim\limits_{x \to a} [f(x) \pm g(x)] = \lim\limits_{x \to a} f(x) \pm \lim\limits_{x \to a} g(x)$$

2. Regra do Produto:
   O limite do produto de duas funções é o produto dos seus limites:

   $$\lim\limits_{x \to a} [f(x) \cdot g(x)] = \lim\limits_{x \to a} f(x) \cdot \lim\limits_{x \to a} g(x)$$

3. Regra do Quociente:
   O limite do quociente de duas funções é o quociente dos seus limites (desde que o limite do denominador não seja zero):

   $$\lim\limits_{x \to a} \frac{f(x)}{g(x)} = \frac{\lim\limits_{x \to a} f(x)}{\lim\limits_{x \to a} g(x)} \quad \text{(se } \lim\limits_{x \to a} g(x) \neq 0\text{)}$$

4. Regra do Multiplicador Constante:
   O limite de uma constante multiplicada por uma função é a constante multiplicada pelo limite da função:

   $$\lim\limits_{x \to a} [c \cdot f(x)] = c \cdot \lim\limits_{x \to a} f(x)$$

5. Regra da Potência:
   O limite de uma função elevada a uma potência é o limite da função elevado a essa potência:

   $$\lim\limits_{x \to a} [f(x)]^n = \left[\lim\limits_{x \to a} f(x)\right]^n$$

Essas propriedades são extremamente úteis para simplificar limites complexos. Por enquanto, você pode utilizá-las como ferramentas sem se preocupar muito com as demonstrações.

Limites Especiais para Memorizar 🧠

Alguns limites aparecem com tanta frequência no cálculo que vale a pena memorizá-los. Aqui estão alguns dos mais importantes:

1. Limite do Seno:

   $$\lim\limits_{x \to 0} \frac{\sin(x)}{x} = 1$$

   Este limite é fundamental na trigonometria e aparece frequentemente em problemas de cálculo.

2. Limite da Exponencial:

   $$\lim\limits_{x \to 0} \frac{e^x - 1}{x} = 1$$

   Essencial ao lidar com funções exponenciais.

3. Limite do Logaritmo Natural:

   $$\lim\limits_{x \to 0} \frac{\ln(1 + x)}{x} = 1$$

   Muito útil para trabalhar com funções logarítmicas.

4. Limite no Infinito:

   $$\lim\limits_{x \to \infty} \frac{1}{x} = 0$$

   Isso mostra que, à medida que $x$ cresce indefinidamente, $\frac{1}{x}$ se aproxima de 0.

5. Limite de Potência no Infinito:
   Para qualquer inteiro positivo $n$,

   $$\lim\limits_{x \to \infty} \frac{1}{x^n} = 0$$

   Essa propriedade generaliza a anterior e é útil para polinômios de grau mais alto.

Por que Aceitar Isso por Enquanto? 🤔

Você pode estar se perguntando: Por que não podemos provar essas propriedades e limites especiais agora? A resposta é simples: essas provas exigem um conhecimento mais aprofundado de cálculo, incluindo conceitos como continuidade, derivadas e a definição formal de limites.

Por enquanto, basta aceitar essas propriedades e limites como ferramentas para resolver problemas. Conforme você avança nos seus estudos, verá as demonstrações e compreenderá melhor a fundamentação teórica por trás delas.

Exercícios para Praticar 🧩

Resolva os seguintes limites:

Respostas para Conferir seu Trabalho ✅

1️⃣ Resolução do limite

Ao tentar substituir diretamente, encontramos:

💡 Dica de Ouro para Limites com Polinômios!

Sempre que você calcular um limite de uma fração polinomial para $( x \to a )$ e encontrar a indeterminação "0/0", preste atenção! 👀 Isso significa que o numerador e o denominador possuem um fator $(x - a)$ em comum.

🔍 O segredo? Basta encontrar uma forma de fatorar ambos e cancelar esse termo, simplificando a expressão! 🧩✂️

Nesse caso, temos:

E, ao fatorarmos, percebemos que esse realmente é o caso:

Portanto, ao cancelarmos os termos $(x - 1)$, obtemos

E podemos tranquilamente substituir $x$ por $1$:

✅ Resposta: $0$

2️⃣ Resolução do limite

Mais uma vez, temos uma indeterminação e aplicamos a fatoração para resolver o problema:

Cancelando $x - 3$, obtemos:

Agora, podemos simplesmente substituir $x = 3$:

✅ Resposta: $6$

3️⃣ Resolução do limite

Este é um limite fundamental da trigonometria, como mostrado na seção de limites especiais:

✅ Resposta: $1$

4️⃣ Resolução do limite

Passo 1: Dividindo todos os termos pelo maior grau de $x$, que é $x^2$:

Passo 2: Como $\frac{5}{x^2} \to 0$ e $\frac{1}{x} \to 0$ quando $x \to \infty$, temos:

✅ Resposta: $\frac{3}{2}$

Continue praticando e, em breve, essas propriedades e limites especiais se tornarão naturais para você! 🚀

Por que os Limites São Importantes? Uma Aplicação Real 🚀

Você pode estar se perguntando: Por que preciso aprender sobre limites? Qual é a relevância disso? Ótima pergunta! Os limites não são apenas conceitos matemáticos abstratos — eles têm aplicações reais, especialmente em física e engenharia. Uma das aplicações mais importantes é o cálculo da velocidade instantânea.

Velocidade Instantânea: A Necessidade dos Limites

Na física, a velocidade é definida como a taxa de variação da posição de um objeto ao longo do tempo. Se você está dirigindo um carro, o velocímetro mostra sua velocidade instantânea — ou seja, quão rápido você está se movendo em um momento específico. Mas como calcular isso?

Seja $s(t)$ a função que representa a posição de um objeto no tempo $t$. A velocidade média entre dois instantes $t = a$ e $t = a + h$ é dada por:

Essa fórmula fornece a velocidade ao longo de um intervalo de tempo $h$. Mas e se quisermos saber a velocidade exatamente no instante $t = a$? Aí entram os limites!

Da Velocidade Média para a Velocidade Instantânea

Para encontrar a velocidade instantânea no tempo $t = a$, fazemos o intervalo de tempo $h$ tender a zero:

Esse limite nos fornece a velocidade exata no instante $t = a$. Parece familiar? Isso é, essencialmente, a definição da derivada de $s(t)$ em $t = a$!

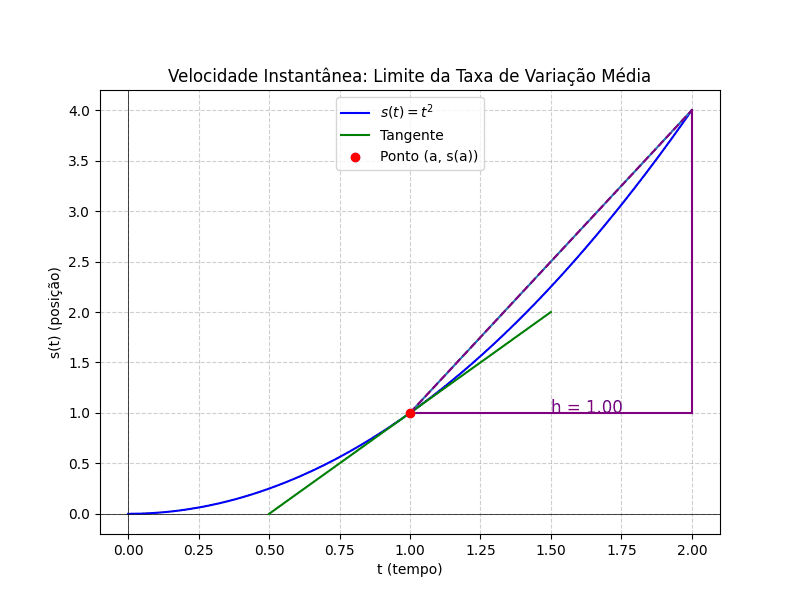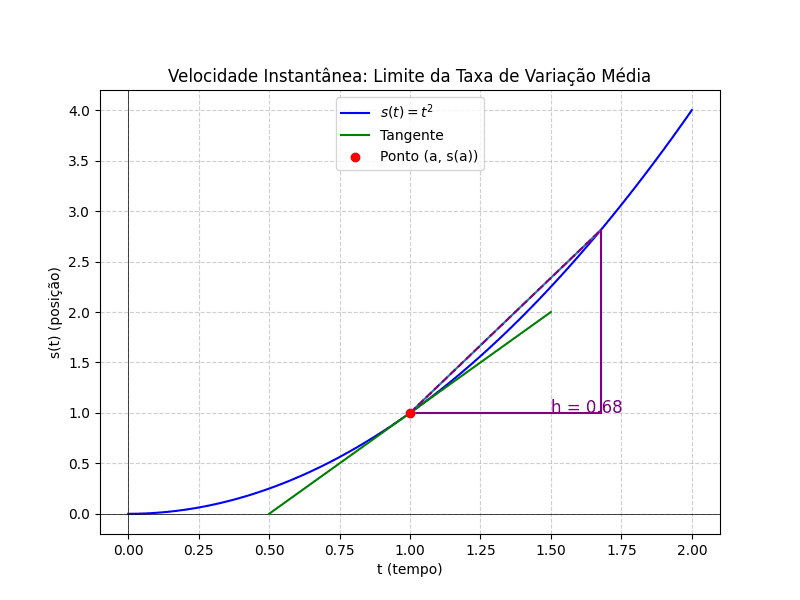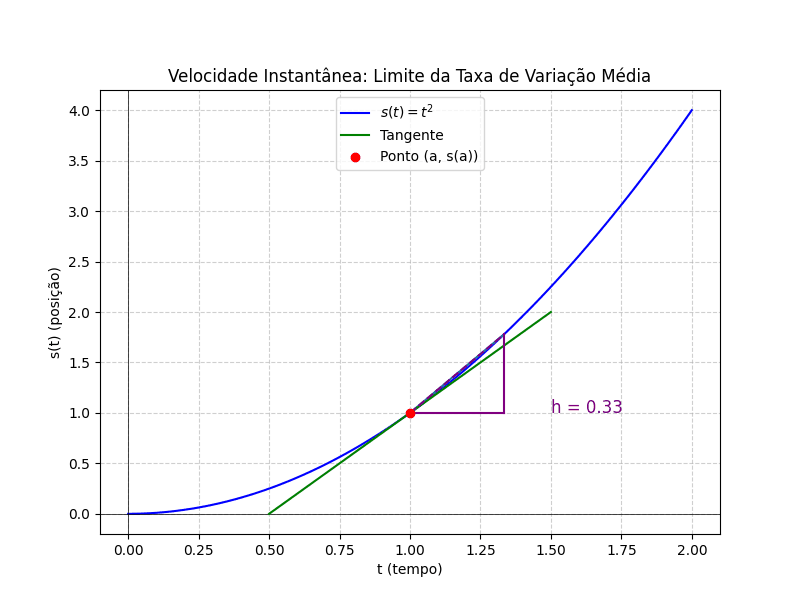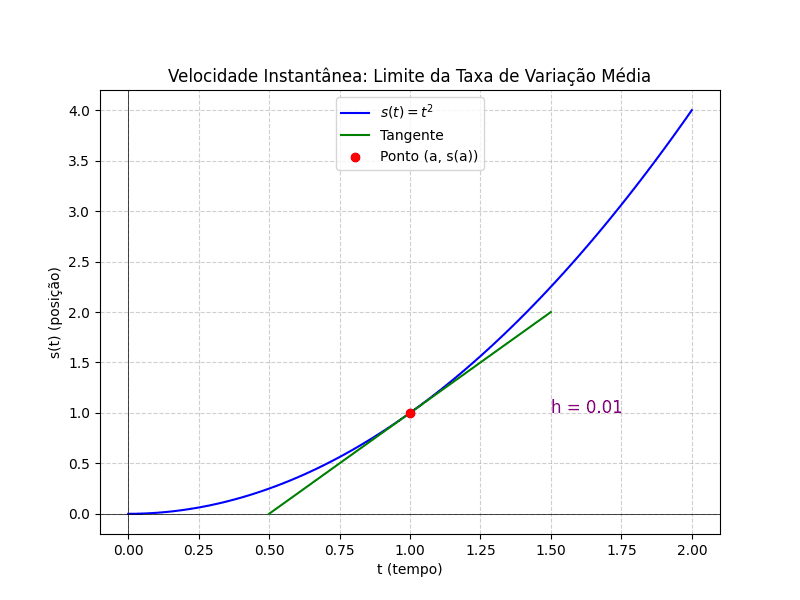
Neste gráfico, podemos observar que, à medida que $h$ diminui, o cálculo da velocidade média se aproxima cada vez mais da reta tangente ao ponto, que representa a velocidade instantânea. Essa reta tangente, no contexto do Cálculo, é conhecida como derivada, e será aprofundada no próximo artigo.

Exemplo: Calculando a Velocidade Instantânea

Vamos tornar isso mais concreto com um exemplo. Suponha que a posição de um objeto no tempo $t$ seja dada por:

Queremos encontrar a velocidade instantânea no instante $t = 2$ segundos.

1. Passo 1: Escrever a Fórmula da Velocidade Média

   $$\text{Velocidade Média} = \frac{s(2 + h) - s(2)}{h}$$

2. Passo 2: Calcular $s(2 + h)$ e $s(2)$

   $$s(2 + h) = (2 + h)^2 + 3(2 + h) + 2 = h^2 + 7h + 12$$ $$s(2) = 2^2 + 3(2) + 2 = 12$$

3. Passo 3: Substituir na fórmula

   $$\text{Velocidade Média} = \frac{(h^2 + 7h + 12) - 12}{h} = h + 7$$

4. Passo 4: Calcular o Limite

   $$\text{Velocidade Instantânea} = \lim\limits_{h \to 0} (h + 7) = 7$$

   Assim, a velocidade instantânea no instante $t = 2$ é 7 metros por segundo.

O Que Vem a Seguir? 📚

No próximo artigo, exploraremos derivadas — o próximo passo natural depois dos limites. Você aprenderá a calculá-las, interpretá-las e aplicá-las em problemas do mundo real. Prepare-se para levar seu entendimento de cálculo ao próximo nível!